The ‘pop-in’ detection

The pop-in detection in the literature

In 2001, Malzbender J. et al. proposed to use the derivative \(dF/dh^{2}\) vs. \(h^{2}\) of the indentation load-displacement data for the pop-in detection [3]. Minima on these curves correspond to pop-in on the load-displacement curve.

In 2004, Juliano T. et al. proposed to extract numerically the derivative behavior from the loading and unloading portions of the load-displacement curves [2]. The numerical first derivative at a depth \(h_\text{x}\) was taken to be the slope of the least-squares fit between load-displacement data points and given as:

(19)\[{\left(\frac{dF}{dh}\right)}_{\text{h}_\text{x}} = \frac{y\left(\sum_{F_{\text{x-(y-1)/2}},h_{\text{x-(y-1)/2}}}^{F_{\text{x+(y-1)/2}},h_{\text{x+(y-1)/2}}}{Fh}\right)-\left(\sum_{h_{\text{x-(y-1)/2}}}^{h_{\text{x+(y-1)/2}}}{h}\right)-\left(\sum_{F_{\text{x-(y-1)/2}}}^{F_{\text{x+(y-1)/2}}}{F}\right)}{y\left(\sum_{h_{\text{x-(y-1)/2}}}^{h_{\text{x+(y-1)/2}}}{h^2}\right)-\left(\sum_{h_{\text{x-(y-1)/2}}}^{h_{\text{x+(y-1)/2}}}{h}\right)}\]

with \(x\) the data points number and \(y\) a positive odd integer number of data points considered.

Juliano T. et al. proposed also to take the derivative at a depth \(h_\text{x}\):

(20)\[{\left(\frac{dF}{dh}\right)}_{\text{h}_\text{x}} = \frac{F_{\text{x+(y-1)/2}}-F_{\text{x-(y-1)/2}}}{h_{\text{x+(y-1)/2}}-h_{\text{x-(y-1)/2}}}\]

In 2014, Askari H. et al. developed the following criteria in his algorithm, to detect a pop-in [1]:

  • Absolute change in depth over 2 lines of data: \(\Delta h = h(i) - h(i-1)\)

  • Forward 2 pts avg - trailing 2 pts average: \(\Delta h = (h(i)+h(i+1))/2 - (h(i-1)+h(i-2))/2\)

  • Forward 3 pts avg - trailing 3 pts average: \(\Delta h = (h(i)+h(i+1)+h(i+2))/3 - (h(i-1)+h(i-2)+h(i-3))/3\)

The absolute step size is the difference beteen two (or more in case averaging is active) consecutive depth readings from the machine. If this step size exceeds a user defined number then it is considered as pop-in.

In her PhD thesis, G. Nayyeri proposed to use the the first derivative at a depth \(h = h_0\) of the load-dispalcement curve, to detect a pop-in [4]:

(21)\[{\left(\frac{dF}{dh}\right)}_{\text{h}_{0}} = {F_{{\text{h}_{0}}+\Delta \text{h}} - F_{\text{h}_{0}} \over \Delta h}\]

The pop-in detection in the PopIn Matlab toolbox

In the PopIn Matlab toolbox, numerous criteria based on the function diff, are implemented to detect pop-in on the load-displacement curve:

  • Criterion 1 - Differences between adjacent depths: \(\Delta h = diff(h) = h(i+1) - h(i)\)

  • Criterion 2 - 2nd differences between adjacent elements (the diff operator is used 2 times): \(\Delta h = diff(diff(h)) = diff(h,2)\)

  • Criterion 3 - 3rd differences between adjacent elements (the diff operator is used 3 times): \(\Delta h = diff(diff(diff(h))) = diff(h,3)\)

  • Criterion 4 - 1st derivative of the load-displacement curve: \(1/(dF/dh) = 1/(diff(F)/diff(h))\)

  • Criterion 5 - 2nd derivative of the load-displacement curve: \(-1/(d^{2}F/dh^{2}) = -1/(diff(dF/dh)/diff(h))\)

  • Criterion 6 - Derivative of the load-displacement curve: \((dF/dh^{2}) = ((diff(F)/diff(h))/diff(h))\)

The 6th criterion is based on the one proposed by Malzbender et al. [3]. Malzbender proposed to plot the 6th criterion as a function of \(h^{2}\) and not as a function of \(h\), like it is proposed in the PopIn toolbox.

When a pop-in occurs, a peak is observed on the plot of differences or derivatives. Peaks anaysis is performed using the function peakdet released by E. Billauer to the public domain (http://www.billauer.co.il/peakdet.html). Only positive peaks are counted. A point is considered a maximum peak if it has the maximal value, and was preceded (to the left) by a value lower by a given delta. The delta value can be set by user from the GUI.

Plots of the different criteria normalized by its maximum as a function of normalized indentation displacement (\(h/max(h)\)).

_images/load-disp_curve_popin_exp.png

Figure 15 Plot of an experimental load-displacement curve displaying a pop-in.

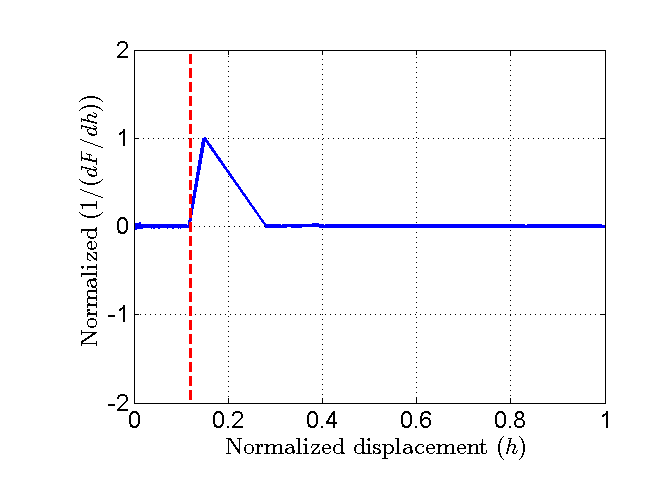
_images/load-disp_curve_popin_diff1.png

Figure 16 Plot of the normalized 1st criterion.

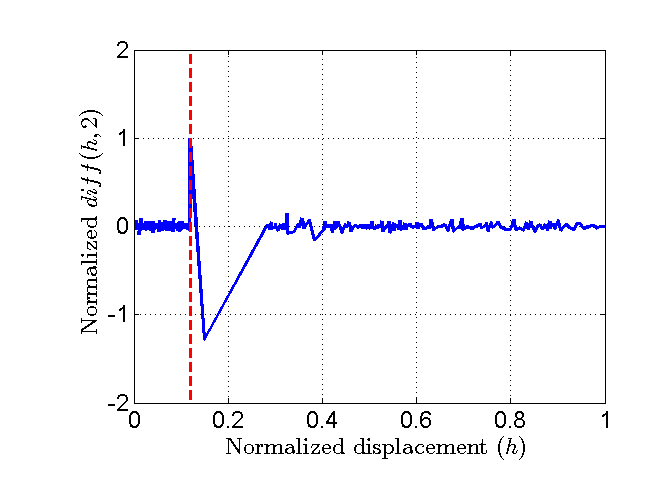
_images/load-disp_curve_popin_diff2.png

Figure 17 Plot of the normalized 2nd criterion.

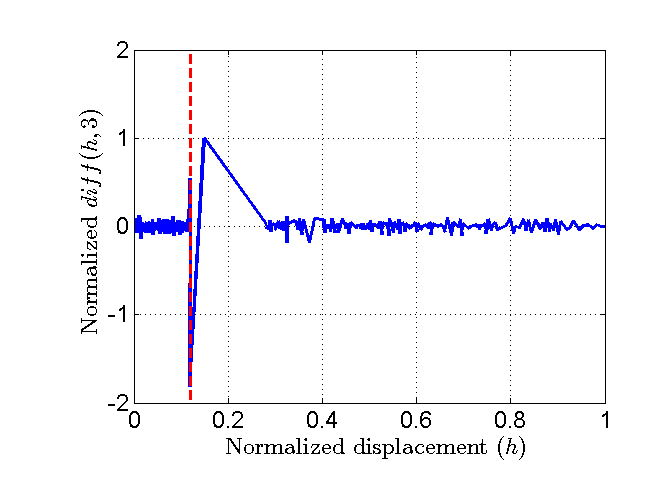
_images/load-disp_curve_popin_diff3.png

Figure 18 Plot of the normalized 3rd criterion.

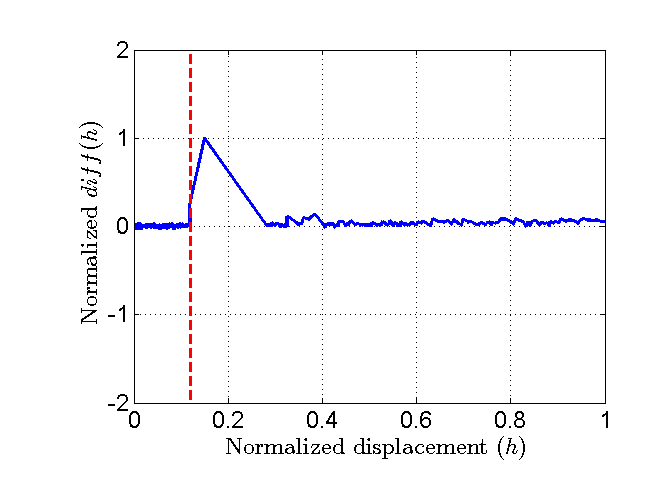
_images/load-disp_curve_popin_dfdh.png

Figure 19 Plot of the normalized 4th criterion.

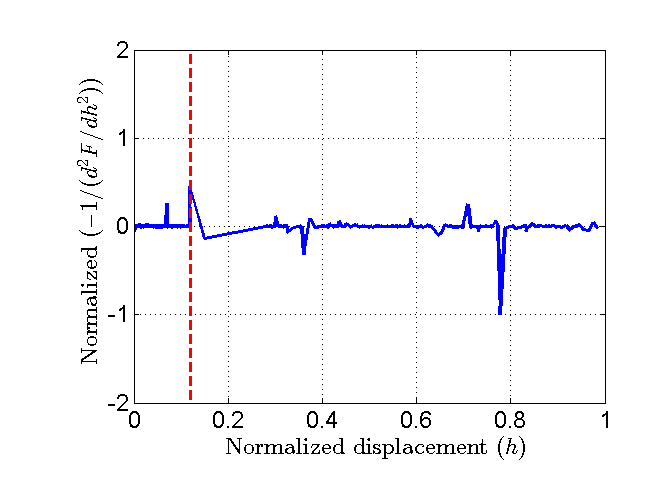
_images/load-disp_curve_popin_d2fdh2.png

Figure 20 Plot of the normalized 5th criterion.

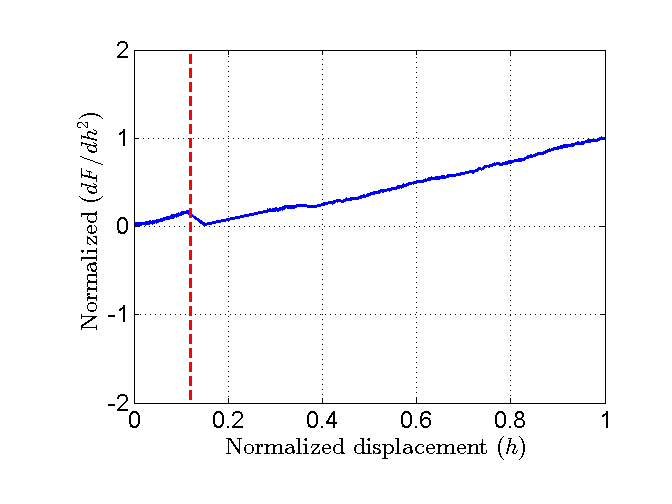
_images/load-disp_curve_popin_dfdh2.png

Figure 21 Plot of the normalized 6th criterion.

References